1. Tổng hợp công thức toán 12 đại số
1.1. Các công thức liên quan tới tam thức bậc 2
a, Định nghĩa
Tam thức bậc hai (một ẩn) là đa thức có dạng f(x) = ax2 + bx + c
Trong đó:
- x: là biến.
- a, b, c: là các số đã cho a≠0.
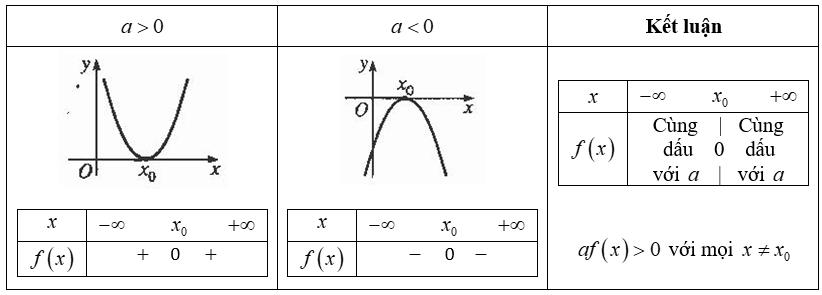
b, Xét dấu tam thức bậc 2
Cho tam thức bậc hai f(x) = af(x) = ax2 + bx + c (a≠0) có biệt thức Δ=b2-4ac
- Nếu Δ<0 thì f(x) luôn cùng dấu với hệ số a với x∈R
- Nếu Δ=0 thì f(x) có nghiệm kép x=−b2a
Khi đó f(x) sẽ cùng dấu với hệ số a với mọi x=−b2a
- Nếu Δ>0, f(x) có 2 nghiệm x1, x2 (x1< x2) và luôn cùng dấu với hệ số a với x ∈(−∞;x1)∪(x2;+∞) và luôn trái dấu với hệ số a với x∈(x1, x2).

>> Tham khảo thêm: Lý thuyết dấu của tam thức bậc hai và bài tập vận dụng
1.2. Bất đẳng thức Cauchy, cấp số nhân, cấp số cộng
a, Bất đẳng thức Cauchy (Cosi)
Định nghĩa:
Bất đẳng thức Cosi hay còn gọi là bất đẳng thức giữa trung bình cộng và trung bình nhân (AM - GM). Cauchy chính là người đã chứng minh được bất đẳng thức AM - GM sử dụng phương pháp quy nạp.
Dạng tổng quát bất đẳng thức cosi:
Cho x1,x2, x3…xn là các số thực không âm khi đó ta có:
- Dạng 1: $frac{x_{1}+x_{2}+...+x_{n}}{n} geq sqrt[n]{x_{1}.x_{2}...x_{n}}$
- Dạng 2: $x_{1}+x_{2}+...+x_{n}geq n.sqrt[n]{x_{1}.x_{2}...x_{n}}$
- Dạng 3: $left ( frac{x_{1}+x_{3}+x_{n}}{n} right )geq x_{1}.x_{2}...x_{n}$
=> Dấu đẳng thức sẽ xảy ra khi và chỉ khi $x_{1}=x_{2}=...=x_{n}$
Cho x1,x2, x3…xn là các số thực không âm khi đó ta có:
Dạng 1: $frac{1}{x_{1}}+frac{1}{x_{2}}+...+frac{1}{x_{n}}geq frac{n^{2}}{x_{1}+x_{2}+...x_{n}}$
Dạng 2: $left ( x_{1}+x_{2}+...x_{n} right )left (frac{1}{x_{1}}+frac{1}{x_{2}}+...+frac{1}{x_{n}} right )geq n^{2}$
=> Dấu đẳng thức sẽ xảy ra khi và chỉ khi $x_{1}=x_{2}=x_{n}$
Ngoài ra còn có các bất đẳng thức cosi đặc biệt:

b, Cấp số nhân
Định nghĩa:
Số hạng tổng quát:
$u_{n}=u_{1}.q^{n-1}, (ngeq 2)$
Ví dụ: Cho cấp số nhân $(u_{n})$ thỏa mãn $u_{1}=5,q=3$. Tính $u_{5}$.
Ta có: $u_{5}=u_{1}q^{4}=5.3^{4}=405$.
Tính chất:

>> Xem thêm: Công thức tính tổng cấp số nhân lùi vô hạn và bài tập
Nắm trọn kiến thức, các công thức và phương pháp giải mọi dạng bài tập Toán thi THPT Quốc gia ngay!

c, Cấp số cộng
Định nghĩa:

>> Tìm hiểu thêm: Cấp số cộng là gì? 5 Công thức cấp số cộng và bài tập
Số hạng tổng quát:
1.3. Phương trình, bất phương trình có chứa giá trị tuyệt đối
Ta có công thức:

Cách giải một số phương trình chứa dấu giá trị tuyệt đối:
- Bước 1: Áp dụng định nghĩa giá trị tuyệt đối sau đó loại bỏ dấu giá trị tuyệt đối.
- Bước 2: Giải phương trình không có dấu giá trị tuyệt đối trước.
- Bước 3: Chọn nghiệm thích hợp cho từng trường hợp đang xét.
- Bước 4: Kết luận nghiệm của phương trình/ bất phương trình.
1.4. Phương trình, bất phương trình có chứa căn
Hiện tại có 4 dạng phương trình chứa căn, bất phương trình chứa căn cơ bản như sau:

1.5. Phương trình, bất phương trình logarit
a, Công thức phương trình logarit

>> Xem thêm:
- 4 cách giải phương trình logarit nhanh gọn, chính xác
- Đầy đủ và chi tiết bài tập phương trình logarit có lời giải
b, Công thức bất phương trình logarit

>> Xem thêm:
- Lý thuyết và bài tập bất phương trình logarit đầy đủ nhất
- Công thức bất phương trình logarit cơ bản, đầy đủ nhất
- Cách giải bất phương trình logarit chi tiết kèm ví dụ cụ thể
- Cách giải bất phương trình logarit chứa tham số cực dễ hiểu
1.6. Lũy thừa và Logarit
Ta có bảng công thức lũy thừa lớp 12:

Ngoài ra, các em có thể tham khảo công thức luỹ thừa của lũy thừa cơ bản và đồ thị hàm số lũy thừa để áp dụng trong các bài toán về lũy thừa.
Và bảng công thức logarit lớp 12:

Ngoài ra còn 1 vài lưu ý khác các em cần lưu ý:

>> Xem thêm: Tổng ôn tập hàm số lũy thừa hàm số mũ và hàm số logarit
Đăng ký ngay để được các thầy cô tổng hợp kiến thức và xây dựng lộ trình đạt 9+ thi THPT Quốc Gia

2. Full công thức toán 12 chủ đề lượng giác
- Công thức lượng giác:

- Phương trình lượng giác thường gặp:
- Hệ thức lượng trong tam giác:
Ta có trong tam giác vuông

Ngoài ra còn có hệ thức liên hệ giữa cạnh và góc trong tam giác vuông:

>> Xem thêm:
- Các công thức nguyên hàm lượng giác cơ bản và bài tập
- Bảng công thức đạo hàm của hàm số lượng giác chi tiết nhất
- Lý thuyết và bài tập đạo hàm hàm số lượng giác 11
- Cách xét tính đơn điệu của hàm số lượng giác và bài tập
3. Đạo hàm, tích phân, hình học, nhị thức Newton
3.1. Đạo hàm
Ta có các công thức tính đạo hàm cơ bản như sau:

>> Xem thêm:
- Chiến trọn từ A - Z kiến thức đạo hàm hàm số mũ
- Lý thuyết và bài tập có lời giải đạo hàm logarit
3.2. Bảng các nguyên hàm

>> Tham khảo thêm: Bảng công thức nguyên hàm đầy đủ nhất
3.3. Diện tích hình phẳng - Thể tích vật thể tròn xoay
Các công thức tính thể tích vật tròn xoay như sau:

Ngoài ra, các em có thể tham khảo thêm công thức tính thể tích khối tròn xoay và thể tích khối trụ tròn xoay kèm bài tập vận dụng cụ thể.
3.4. Phương pháp tọa độ trong mặt phẳng

3.5. Phương pháp tọa độ trong không gian

>> Tham khảo thêm: Bài toán trong không gian với hệ tọa độ Oxyz cho 3 điểm
3.6. Nhị thức Niuton
>> Tham khảo thêm: Lý thuyết Nhị thức Niu Tơn kèm các dạng toán có đáp án

4. Công thức toán 12 hình học giải tích trong không gian
4.1. Tích có hướng của 2 vec tơ
Một số công thức tính tích có hướng của 2 véc tơ cần phải ghi nhớ:

>> Xem thêm: Lý thuyết và bài tập tích của vecto với một số
4.2. Phương trình mặt cầu


>> Tham khảo thêm: Lý thuyết phương trình mặt cầu và các dạng bài tập
4.3. Phương trình mặt phẳng

>> Xem thêm:
- Lý thuyết phương trình mặt phẳng và các dạng bài tập
- Cách viết phương trình mặt phẳng trung trực của đoạn thẳng
4.4. Phương trình đường thẳng

4.5. Vị trí giữa mặt phẳng và mặt cầu

4.6. Khoảng cách từ điểm đến đường thẳng

4.7. Góc giữa 2 đường thẳng
>> Xem thêm: Định nghĩa và cách xác định góc giữa 2 mặt phẳng
4.8. Góc giữa đường thẳng và mặt phẳng
>> Xem thêm: Cách xác định góc giữa đường thẳng và mặt phẳng trong không gian
4.9. Hình chiếu và điểm đối xứng
Bài viết đã cung cấp những kiến thức rất đầy đủ toàn bộ công thức toán 12. Ngoài ra, các em có thể truy cập ngay Vuihoc.vn để đăng ký tài khoản hoặc liên hệ trung tâm hỗ trợ để nhận thêm nhiều bài học hay và ôn tập kiến thức Toán 12 để chuẩn bị được kiến thức tốt nhất cho kỳ thi THPT quốc gia sắp tới nhé!
>> Xem thêm:
- Tổng hợp công thức toán hình 12 đầy đủ dễ nhớ nhất
- 8 cách học toán 12 bứt phá đạt điểm 8+ cho người mất gốc
- Đầy đủ lý thuyết và bài tập số phức modun
