
Công thức tính diện tích hình thang, chu vi hình thang
1. Công thức tính diện tích hình thang
Trước tiên tính công thức chung của hình thang chúng ta sẽ có công thức: trung bình cộng 2 cạnh đáy nhân với chiều cao giữa 2 đáy.
Theo như công thức trên diện tích hình thang định nghĩa bằng lời là Diện tích của hình thang bằng chiều cao nhân với trung bình cộng của tổng hai cạnh đáy.
Còn có bài thơ về tính diện tích hình thang khá dễ nhớ như sau:
Muốn tính diện tích hình thang
Đáy lớn đáy nhỏ ta đem cộng vào
Cộng vào nhân với chiều cao
Chia đôi lấy nửa thế nào cũng ra
Cách tính diện tích hình thang cân
Ngoài việc áp dụng công thức như tính hình thang bình thường, bạn cũng có thể chia nhỏ hình thang cân ra để tính diện tích từng phần rồi cộng lại với nhau.
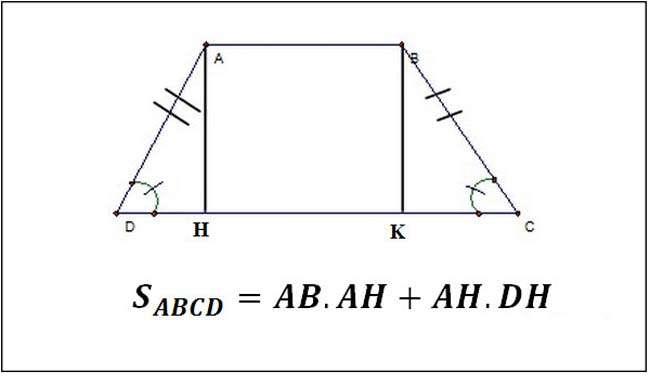
Giả dụ, hình thang cân ABCD có 2 cạnh bên AD và BC bằng nhau. Đường cao AH và BK, hình thang sẽ được chia ra thành 1 hình chữ nhật ABKH và 2 hình tam giác là ADH và BCK. Áp dụng công thức tính diện tích hình chữ nhật cho ABHK và diện tích tam giác cho ADH và BCK sau đó cộng tất cả diện tích để tìm diện tích hình thang ABCD.
2. Công thức tính chu vi hình thang, cách tính chu vi hình thang
P = a + b + c + d
Theo như công thức trên chu vi hình thang được định nghĩa theo lời: Chu vi hình thang bằng tổng độ dài của hai đáy và cạnh bên.
Hình thang vuông: Có một cạnh bên vuông góc với hai đáy, cạnh bên đó chính là chiều cao hình thang vuông. Khi tính diện tích hình thang vuông ta tính như cách tìm hình thang.
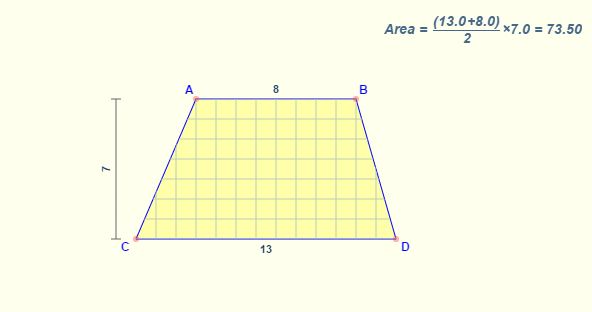
Ví dụ cụ thể giả sử ta có hình thang ABCD với các cạnh AB = 8, cạnh đáy CD = 13, chiều cao giữa 2 cạnh đáy là 7 thì chúng ta sẽ có diện tích hình thang là:
S(ABCD) = (8+13)/2 x 7 = 73.5
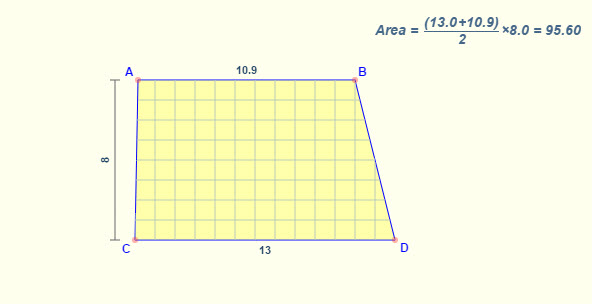
Tương tự ví dụ với trường hợp hình thang vuông chúng ta cũng tính tương tự
S(ABCD) = (AB + CD)/2 x AC = (10.9 + 13)/2 x 8 = 95.6
3. Tính diện tích hình thang khi biết 4 cạnh
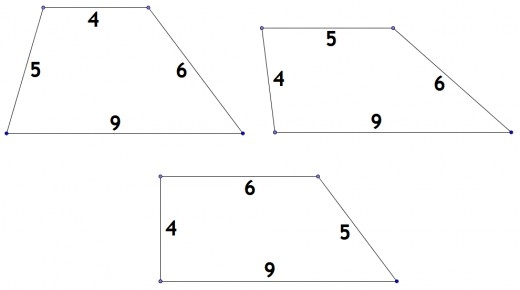
Thực tế nếu bài toán đưa ra câu hỏi cách tính 4 cạnh của hình thang khi biết 4 cạnh thì sẽ không có đáp án chính xác vì chỉ biết 4 cạnh thì có rất nhiều trường hợp xay ra và diện tích cũng khác nhau, các bạn có thể hình dung ví dụ hình thang dưới đây có 4 cạnh 4 5 6 9 có thể vẽ 3 dạng hình khác nhau với diện tích khác nhau.
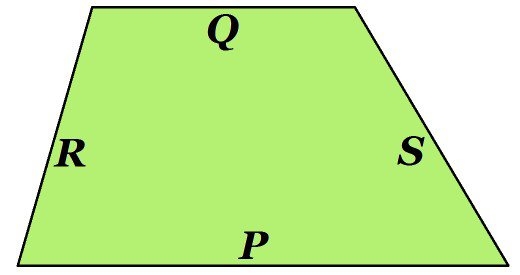
 Tuy nhiên nếu bài toán cho thêm vài dữ kiện ví dụ như tính diện tích hình thang khi biết độ dài 4 cạnh và có nõi rõ cạnh đáy là cạnh nào thì có thể tính được diện tích hình thang, ví dụ chúng tao có các cạnh đấy Q P, trong đó cạnh đáy P dài hơn và 2 cạnh bên R và S.
Tuy nhiên nếu bài toán cho thêm vài dữ kiện ví dụ như tính diện tích hình thang khi biết độ dài 4 cạnh và có nõi rõ cạnh đáy là cạnh nào thì có thể tính được diện tích hình thang, ví dụ chúng tao có các cạnh đấy Q P, trong đó cạnh đáy P dài hơn và 2 cạnh bên R và S.
Thì có thể áp dụng công thức tính diện tích hình thang như sau:
Ngoài ra trong trường hợp tính diện tích hình thang khi biết các cạnh các bạn có thể tách ra thành 2 tam giác và 1 hình chữ nhật hoặc kẻ thêm đường giao giữa 2 cạnh bên và áp dụng công thức Heron tính diện tích tam giác và suy ra được diện tích hình thang. Công thức trên cũng được hình thành từ cách này.
4. Bài tập hình thang, diện tích hình thang
Câu 1. Cho hình thang ABCD có độ dài đường cao là 4,2 dm, diện tích = 36,12 dm2 và đáy lớn CD dài hơn đáy bé AB là 7,8 dm. Kéo dài AD và BC cắt nhau tại E. Biết AD = 3/5 DE. Hỏi diện tích hình tam giác ABE là bao nhiêu?
Câu 2. Cho hình thang ABCD. Bốn điểm M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Biết diện tích tứ giác MNPQ là 115 cm2. Tính diện tích hình thang ABCD.
Câu 3. Cho hình thang vuông ABCD (góc A, D là góc vuông) có AB=4cm, DC=5cm, AD=3cm. Nối D với B được hai hình tam giác ABD và BDC.
a) Tính diện tích hình tam giác đó.
b) Tính tỉ số phần trăm của diện tích hình tam giác ABD và diện tích hình tam giác BDC.
Câu 4. Tính diện tích hình thang có :
a). Đáy lớn 8m; đáy bé 75dm; chiều cao 32dm.
b). Đáy lớn 1,9m; đáy bé 1,3m; chiều cao 0,9m.
c). Đáy lớn 2/3m; đáy bé 1/2m; chiều cao 3/5m.
Câu 5. Tính chiều cao hình thang có:
a). Diện tích 30cm²; đáy lớn 8cm và đáy bé 0,4dm.
b). Diện tích 6,4 dm²; đáy lớn 1,8dm; đáy bé 1,4dm.
c). Diện tích 3/4m²; đáy lớn 1/4m và đáy bé 1/8m.
Câu 6. Tính tổng hai đáy hình thang có:
a). Diện tích 3,6 dam²; chiều cao 1,2dam.
b). Diện tích 3/4m²; chiều cao 2/3m.
c). Diện tích 2400cm²; chiều cao 3,8dm.
Câu 7. Một miếng đất hình thang có đáy bé 18m và bằng ¾ đáy lớn. Tính diện tích miếng đất hình thang?
Câu 8. Một thửa ruộng hình thang vuông có cạnh bên vuông góc với 2 đáy dài 30,5m; đáy lớn 120,4m; đáy bé 79,6m.
a. Tính diện tích thửa ruộng bằng dam²
b. Trung bình 100dam2 thu được 65,2kg thóc. Hỏi trên cả thửa ruộng thu được bao nhiêu kg thóc?
Câu 9. Một hình thang có tổng hai đáy 110cm. Tổng của đáy lớn và chiều cao 114cm. Tổng của đáy bé và chiều cao là 68cm. Tính diện tích hình thang?
Câu 10. Một hình thang có đáy bé 2,8dm.Đáy lớn bằng 7/3 đáy bé và bằng 5/3 chiều cao. Tính diện tích hình thang.
Câu 11. Một thửa ruộng hình thang có đáy lớn 140m và bằng 4/3 đáy bé, chiều cao 56,4m. Tính ra cứ 5dam² thì thu hoạch được 320kg thóc. Hỏi cả thửa ruộng thu được bao nhiêu tấn thóc?
Câu 12. Một miếng đất hình thang có tổng đáy lớn, đáy bé và chiều cao là 90m. Đáy bé bằng 3/4 đáy bé; chiều cao bằng ½ đáy lớn. Biết rằng cứ 2 dam² thì cần phải bón 50kg phân. Hỏi bón cả thửa ruộng thì cần phải có bao nhiêu tạ phân?
Câu 13. Một thửa ruộng hình thang có đáy lớn 75,6m; đáy bé 62,4m và chiều cao 40m. Biết rằng 2/5 diện tích thửa ruộng trồng ngô, 1/3 diện tích trồng khoai, còn lại trồng đậu phộng. Tính diện tích trồng mỗi loại cây trên?
Các bạn có thể luyện tập các bài tập về diện tích hình thang sau: 31 Bài Toán về diện tích hình thang.
Công thức tính diện tích hình thang, chu vi hình thang cực dễ nhớ. Cách tính cũng như ví dụ về chu vi hình thang, diện tích hình thang để các em học sinh nắm chắc giải các dạng toán liên quan.
Hình thang là hình gặp khá nhiều trong cuộc sống hằng ngày. Nếu như việc tính chu vi hình thang thì khá dễ nhớ bằng tổng 4 cạnh thì công thức tính diện tích hình tháng lâu ngày có thể bạn sẽ khó nhớ. Các bạn có thể tham khảo công thức tính diện tích hình thang, chu vi hình thang và các bài tập liên quan sau đây.
- Công thức tính chu vi hình chữ nhật và diện tích hình chữ nhật
- Công thức tính chu vi hình tròn và diện tích hình tròn
5. Hình thang là gì
Khái niệm: Hình thang là một tứ giác lồi có hai cạnh đáy song song, 2 cạnh còn lại được gọi là hai cạnh bên.
Hình thang vuông là hình thang có một góc vuông. Cạnh bên vuông góc với hai đáy cũng chính là chiều cao của hình thang.
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. 2 cạnh bên của hình thang cân bằng nhau và không song song với nhau.
6. Giải Bài tập về hình thang lớp 5
- Bài tập tính diện tích hình thang lớp 5 Nâng cao có đáp án
- Giải vở bài tập Toán 5 bài 90: Hình thang
- Giải vở bài tập Toán 5 bài 91: Diện tích hình thang
- Giải vở bài tập Toán 5 bài 92: Luyện tập Diện tích hình thang
- Giải bài tập trang 91, 92 SGK Toán 5: Hình thang
- Giải bài tập trang 93, 94 SGK Toán 5: Diện tích hình thang
- Giải bài tập trang 94, 95 SGK Toán 5: Luyện tập chung diện tích hình thang
Để học tốt Toán lớp 5, các dạng bài tập từ cơ bản đến nâng cao, các em tham khảo các chuyên mục sau:
- Toán lớp 5
- Giải bài tập Toán lớp 5
- Giải Vở Bài Tập Toán 5
- Toán lớp 5 Nâng cao
Các công thức tổng hợp rất quan trọng trong các kì thi, các em học sinh có thể tham khảo chi tiết các công thức sau đây:
- Tóm tắt Công thức Toán Tiểu học dễ học thuộc
- Công thức hình học ở tiểu học
- Công thức Toán cơ bản và nâng cao lớp 5
Link nội dung: http://thoitiet247.edu.vn/chu-vi-hinh-thang-a10646.html