What is an Angle?
An angle is formed when two straight lines or rays meet at a common endpoint. The common point of contact is called the vertex of an angle. The word angle comes from a Latin word named ‘angulus,’ meaning “corner.”
Symbol of Angle
The symbol ∠ represents an angle. Angles are measured in degrees (°) using a protractor.
For example, 45 degrees is represented as 45°
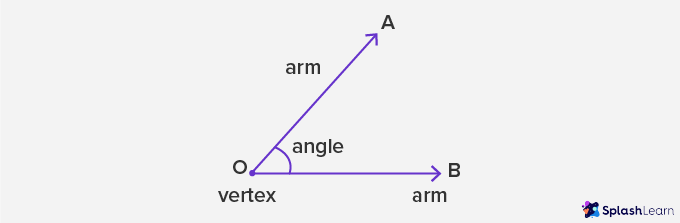
Parts of Angles
- Vertex: A vertex is a corner of an angle, a point where two lines/sides meet. O is the vertex in the given figure.
- Arms: The two sides of the angle, joined at a common endpoint. OA and OB are arms of an angle.
- Initial Side: Also known as the reference line, a straight line from where an angle is drawn. OB is the reference line.
- Terminal Side: The side up to which the angle measurement is done. In the given diagram below, OA is the terminal side.
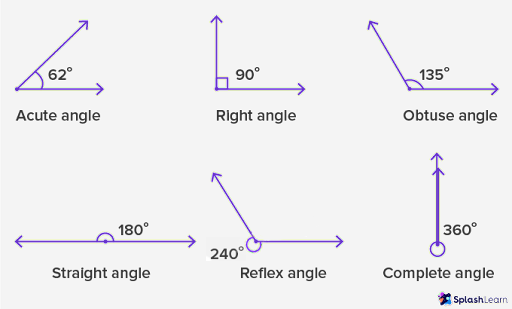
Types of Angles
Based on their measurements, here are the different types of angles:
- An acute angle measures less than 90° at the vertex.
- An obtuse angle is between 90° and 180°.
- A right angle precisely measures 90° at the vertex.
- An angle measuring exactly 180° is a straight angle.
- A reflex angle measures between 180°- 360°.
- `A complete angle measure equals 360°.`A complete angle measure equals 360°.
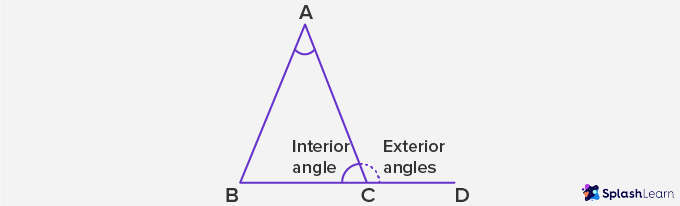
Interior and Exterior Angles:
Interior angles: Interior Angles are the angles formed within or inside a shape.
Here, ∠ABC, ∠BCA and ∠CAB are interior angles.
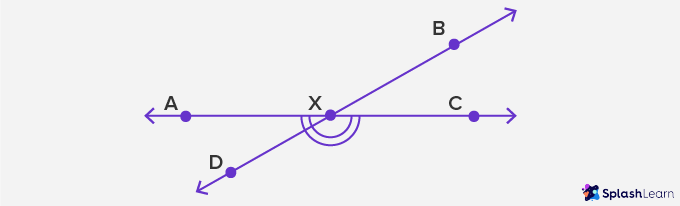
Exterior angles: Exterior angles are the angles formed outside a shape, between any side of a shape and an extended adjacent side. Here, ∠ACD is an exterior angle.
Complementary and Supplementary Angles:
Complementary angles: Angles that add up to 90° (a right angle) are called complementary angles.
Here, ∠BXC and ∠CXD are complementary angles.
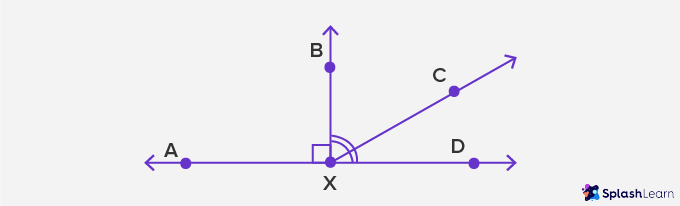
Supplementary angles: Angles that add up to 180° (a straight angle) are called supplementary angles.
Here, ∠AXD and ∠CXD are supplementary angles.
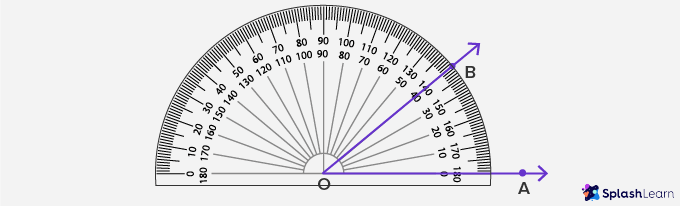
How to Construct an Angle (using protractor)
- Draw a ray OA of any length.
- Now, place the protractor at that point, and its midpoint should touch the marked point O.
- Now mark the point as B on the top circular part of a protractor, according to the preferred angle for example 40°.
- Draw a straight line joining those two points, O and B.
- Mark the degree of the angle made where two sides of the straight line intersect.
Real-life Application of Angles
- Engineers construct buildings, bridges, houses, monuments, etc., using angle measurement.
- Athletes use its concept in sports to enhance their performance.
- Carpenters use it to make equipment like doors, chairs, sofas, tables, etc.
- Artists use their measurement knowledge to sketch or create art pieces.
- Wall clocks use the concept of angles to show time with hour and minute hands.
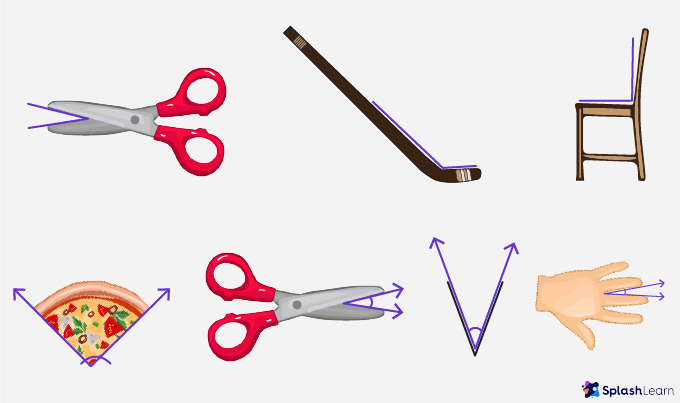
Angles Around Us
There are many daily life examples of an angle, such as cloth-hangers, arrowheads, scissors, partly opened doors, pyramids, edge of a table, the edge of a ruler, etc.

Solved Examples On Angles
Example 1: Find missing angle x in the figure.
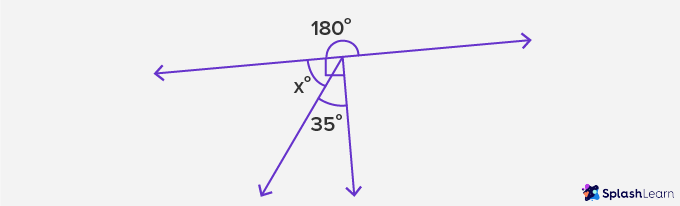
Solution:
We can see a ∠x + 35° = 90°
∠x = (90 - 35)° = 55°
Example 2: Solve for x.
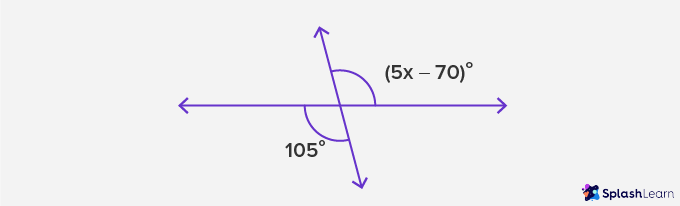
Solution:
5x - 70 = 105 (alternate angles)
5x = 175
Therefore, x = 35°
Example 3: In a triangle ABC, ∠A = 90 and ∠B = 30. Find ∠C.
Solution:
The sum of all 3 interior angles of a triangle is equal to 180°. Hence, 90° + 30° + x = 180°.
Solve for x
x = 180 - (90 + 30) = 60°.
